Wir kommen um den Urknall wohl nicht herum...Wie man den Kosmos modelliert, II

 Wir haben am 5.7. die drei Grundannahmen der Kosmologie kennengelernt:

Isotropie, Kopernikanisches Prinzip und die Gültigkeit der Allgemeinen Relativitätstheorie ART.

Wie man den Kosmos modelliert, Teil II

Das zentrale Element der ART ist die Feldgleichung:

Die Metrik gibt an, wie den Raum-Zeit Koordinaten messbare Abstände zugeordnet werden können. In der euklidischen Metrik gilt z.B. der Satz des Pythagoras: c² = a² + b².

Würde der Lehrsatz die Form haben c² = a² + ab +b², so müsste man das Koordinatensystem auf eine andere Weise mit Abständen beschriften. Die Metrik hätte die Kurzform (1,0,1,1), vergl. mit dme letzten Post dieser Reihe.

Der Krümmungstensor (auch Ricci-Tensor genannt) beschreibt die Auswirkung der vierdimensionalen Raum-Zeit-Krümmung auf einen zweidimensionalen Bereich, und zwar dem Bereich, in dem auch die Metrik angewendet wird.

In diesem Bereich wirken sich auch Energie, Masse und Impuls aus.

Die Feldgleichung ist eigentlich ein Gleichungssystem. Jede Gleichung enthält andere Kombinationen aus den vier Raum-Zeit-Dimensionen zu neuen zweidimensionalen Bereichen.

Unter den oben genannten Voraussetzungen kann man daraus für eine bestimmte Metrik (Robertson-Walker-Metrik) zwei relativ einfache Gleichungen herleiten, es sind die Friedmanngleichungen, gefunden 1922 vom Mathematiker Alexander Friedmann:

die erste ist die Umschreibung der Energieerhaltung und die zweite bedeutet letztlich das Gleiche wie F = m*a.

Diese Differenzialgleichungen verknüpfen den Skalenfaktor R mit seiner zeitlichen Änderung dR/dt.

Damit  kann man den Skalenfaktor R(t) ausrechnen, sozusagen die zeitliche Entwicklung von Abständen im Kosmos.

Die Gleichungen kann man auch ohne die ART, allein aus den Newtonschen Gesetzen herleiten. Man erhält aber dann nicht die Auswirkungen der Dunklen Energie, denn die gibt es bei Newton nicht.

Hier zur Erbauung die 1.Friedmanngleichung

Die zeitliche Entwicklung nennen wir eine parabolische Expansion (beschrieben durch k = 0). Der Urschwung ist erst in unendlich langer Zeit ausgeglichen, die Expansion geht ewig.

Nun verallgemeinern wir: Unser Kosmos kann auch eine wachsende (k = -1, hyperbolische Expansion, die nie zum Stillstand kommt)) oder eine fallende Gesamtenergie (k = +1, elliptische Expansion, der Kosmos steht irgendwann still und kontrahiert wieder) besitzen. 

Und hier die 2.Friedmanngleichung:

In den Friedmann-Gleichungen kommt keine Raumkrümmung vor. Berechnet man mögliche Raumkrümmungen mit Hilfe der ART, so erhält man auch wieder nur 3 Fälle. Das liegt an der Forderung der maximal möglichen Symmetrie des Kosmos.

k kann deshalb auch nur die Werte -1, 0 und +1 annehmen.

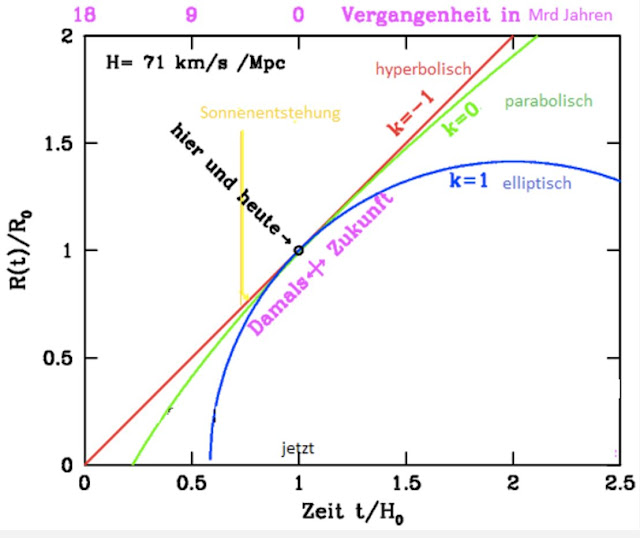
Zu jeder Expansionsform ergibt sich dann eine bestimmte Raumform:

k=0: Die parabolische Expansion besitzt den euklidischen, ungekrümmten Raum.

k= -1: Die  hyperbolische Expansion besitzt den negativ gekrümmten Raum.

k = +1: Die elliptische Expansion besitzt den positiv gekrümmten, in sich geschlossenen Raum.

Wie gesagt, die Gleichungen muss man so nicht verstehen. Man sollte nur wissen, dass sich die drei grundlegenden Formen der Raumkrümmung (parabolisch, elliptisch, hyperbolisch) den drei Grundformen der Expansion (unendlich lange, umkehrend, ewig anwachsend) eindeutig zuordnen kann.

Das fasst das folgende Bild zusammen:

Was für unser Thema spannend ist:

Bei der Auswahl geeigneter Parameter lassen die Friedmanngleichungen eine Entwicklung zu, die nicht bei R(0) = 0 beginnt, also ohne Urknall auskommt.

Können wir also auf den Urknall verzichten?

Mehr im nächsten Post zu dieser Reihe.