Im letzten Post hatten wir die vier möglichen Fälle erwähnt:
1) Sender entfernt sich vom Empfänger
2) Sender läuft auf Empfänger zu
3) Empfänger entfernt sich vom Sender
4) Empfänger kommt auf Sender zu
Zu jeder dieser Fälle gibt es eine Formel. Dabei muss unterschieden werden, ob sich der Sender oder der Empfänger bewegt.
An einem einfachen Beispiel wird deutlich, dass man bei Schall zwischen der Bewegung von Sender und Empfänger unterscheiden muss:
Bewegt sich der Empfänger mit Schallgeschwindigkeit vom Sender weg, so hört er nichts. Totale Ruhe!
Bewegt sich der Sender mit Schallgeschwindigkeit vom Empfänger weg, so hört man sogar sehr viel: es gibt einen Überschallknall.
Die Formeln für den Dopplereffekt bei Schall stehen in der Formelsammlung.
Astronomen beschäftigen sich nicht mit Schall, sondern mit Licht...und bei Licht ist alles viel einfacher:
- Die Lichtgeschwindigkeit ist immer gleich groß, egal ob sich Sender oder Empfänger bewegen.
- Man muss nicht zwischen der Bewegung von Sender und Empfänger unterscheiden. Es kommt nur auf die Relativgeschwindigkeit an.
Das hat natürlich auch einen Nachteil: denn nun kann man nicht mehr unterscheiden, woher die Wellenlängenänderung kommt...durch Bewegung des Sternes, durch die Bewegung der Erde oder duch beides
Fassen wir zusammen:
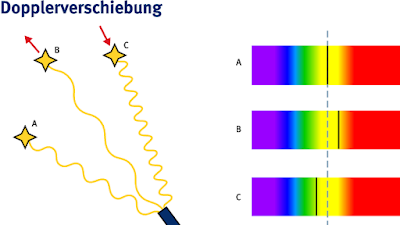
Eine Verlängerung der Wellenlänge (niedrigere Frequenz) bedeutet bei Licht eine Rotverschiebung, eine Verkürzung der Wellenlänge eine Blauverschiebung.
Entfernen sich Lichtquelle und Beobachter voneinander, so sind alle Wellenlängen nach Rot verschoben.
Kommen sie aufeinander zu, so gib es eine Blauverschiebung.
Die Farben der Sterne kann man damit aber so, wie es Doppler wollte, nicht erklären. Dazu sind Sterne zu langsam.
 |
| aus: Welt der Physik |
Hier nun die einfache Formel für den Dopplereffekt bei Licht im nicht-relativistischen Fall (v<<c):
Δλ / λ = v / c
Für v<<c gilt: Die Wellenlängenänderung Δλ verhält sich zur Wellenlänge λ wie die Relativgeschwindigkeit v zur Lichtgeschwindigkeit c.
Ganz wichtig: v ist hierbei die Bewegungskomponente in Blickrichtung!
Bewegungsanteile quer zur Blickrichtung machen sich im Dopplereffekt nicht bemerkbar.
In der Astronomie gibt es nur wenig Fälle, bei denen die Relativgeschwindigkeit an die Lichtgeschwindigkeit herankommt. Da muss man dann noch die Zeitdilatation verwenden.
Es gibt dann sozusagen zwei Dopplereffekte:
Durch die Zeitdilatation werden alle Frequenzen vergrößert, es gibt also eine Rotverschiebung. Diese Rotverschiebung tritt unabhängig von der Bewegungsrichtung auf, also auch bei Bewegungen senkrecht zur Blickrichtung.Das nennt man dann den transversalen Dopplereffekt.
Der "normale" Effekt durch Stauchung oder Streckung der Wellen tritt weiterhin nur in Blickrichtung auf, natürlich zusammen mit der Zeitdilatation. Das nennt man den longitudinalen Dopplereffekt.

Keine Kommentare:
Kommentar veröffentlichen
Kommentar eingeben